Design of Experiments

 Design of Experiments(DOE)

  • A statistics-based approach to designing experiments
  • A methodology to obtain knowledge of a complex, multivariable process with the fewest trials possible.
  • An optimisation of the experimental process itself.
  • The backbone of any product design as well as any process/ product improvement efforts.
During the tutorial session on Design of Experiments, I learnt that the objective of Design of experiments is to understand the process by determining which factors are most influential on Output.

To gave us a better understanding and practice on Design of Experiments, we are tasked to complete 3 pre-practical task of analyzing experiment data using graphical method such as Full and Fractional Factorial graph. Through this activity, we had a better understanding and able to rank them in the order of most significant factors. 

Next, we were assigned to complete the individual case study for Design of Experiments. Being the CFO(Chief Financial Officer) I was task to work on case study 1. 

Case Study 1:

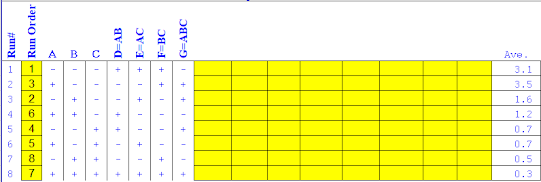
What could be simpler than making microwave popcorn? Unfortunately, as everyone who has ever made popcorn knows, it’s nearly impossible to get every kernel of corn to pop. Often a considerable number of inedible “bullets” (unpopped kernels) remain at the bottom of the bag. What causes this loss of popcorn yield? In this case study, three factors were identified: 

1. Diameter of bowls to contain the corn, 10 cm and 15 cm
2. Microwaving time, 4 minutes and 6 minutes
3. Power setting of microwave, 75% and 100%  

The factors 

Factor A= diameter
Factor B= microwaving time
Factor C= power


 Full Factorial data analysis
Arrange the data in order into the given excel template.

On excel, select insert, select 2-D line graph


After the values is selected, this is how the graph of full factorial looks like:

Ranking of factors:
  1. Factor C (power)
  2. Factor B (microwaving time)
  3. Factor A (Diameter)
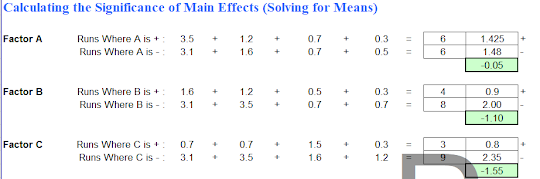
With 1 being the most significant factor and 3 the least significant factor.

Effects of single factor:
  • When the diameter of bowl(factor A) increases from 10cm(-) to 15cm(+), the bullet formed decreases from 1.48g to 1.425g
  • When the microwaving time(factor B) Increases from 4minutes(-) to 6minutes(+), the bullets formed decreases from 2.0g to 0.9 g.
  • When the Power setting of microwave (factor C) increases from 75%(-) to 100%(+), the bullets formed decreases from 2.35g to 0.8g

 Conclusion
  • For factor A, when the bowl diameter increases, the bullets formed decreases but it is not as significant as compared to the others factors. Hence, it is represented in the graph with the least steep gradient.
  • For factor B, when microwaving time increases, it increases the tendency of the corn being pop which reduced the amount of bullets formed. This factor is more significant than Factor A hence it is represented by a line steeper than Factor A.
  • For Factor C, When the power of the microwave increases this allows more heat to be gained and hence increases the number of corn being popped which reduces the mass of bullets formed. Being the most significant factor, the line that represent Factor C is the steepest line  

  • Interaction effects of factors with full factorial graph
Interaction effect of AxB
At low B, the average effect of low A = (3.1+0.7)/2=1.9
At low B, the average effect of high A = (3.5+0.7)/2=2.1
At low B, total effect of A= (2.1-1.9)=0.2
At high B, the average effect of low A = (1.6+0.5)/2=1.05
At high B, the average effect of high A = (1.2+0.3)/2=0.75
At high B, total effect of A= (0.75-1.05)=-0.3
Conclusion: From the graph above, The gradient of both lines are different (one is + and the other is -). Therefore there’s a significant interaction between A and C 


Interaction effect of AxC
At low C, the average effect of low A = (1.6+3.1)/2=2.35
At low C, the average effect of high A = (3.5+1.2)/2=2.35
At low C, total effect of A= (2.35-2.35)=0
At high C, the average effect of low A = (0.7+0.5)/2=0.6
At high C, the average effect of high A = (0.7+0.3)/2=0.5
At high C, total effect of A= (0.5-0.6)=-0.1
Conclusion: The gradient of both lines are different by a little margin. Therefore there’s an interaction between A and B, but the interaction is small. If both lines are parallel, then there’s NO interaction


Interaction effect of BxC
At low C, the average effect of low B = (3.5+3.1)/2=3.3
At low C, the average effect of high B = (1.6+1.2)/2=1.4
At low C, total effect of B= (1.4-3,3)=-1.9
At high C, the average effect of low B = (0.7+0.7)/2=0.7
At high C, the average effect of high B = (0.5+0.3)/2=0.4
At high C, total effect of B= (0.4-0.7)=-0.3

Conclusion: The gradient of both lines are negative and different values. Therefore there’s a significant interaction between B and C
Link to excel file(for better view of graph please download the file)


Fractional Factorial Data Analysis
Fractional Factorial Data Analysis have fewer than all possible treatments are chosen to still provide sufficient information to determine the factor effect. Also, Fractional Factorial is more efficient and resource-effective, but having the risk of missing information. For this Fractional Factorial Data Analysis, it is being scaled down from 8 main effect to 4 main effect with factors and number of run remains the same. The run number I have selected to conduct the Fractional Factorial Data Analysis is run number 1,4,6 and 7.

I used the same excel template given for the Fractional Factorial Data Analysis.
Fractional Factorial graph:
Ranking of factors from most significant to the least significant:
  1. Factor C (power)
  2. Factor B (microwaving time)
  3. Factor A (Diameter)
Effects of each factors:
  • When the diameter of bowl(factor A) increases from 10cm(-) to 15cm(+), the bullet formed decreases from 1.8g to 0.95g
  • When the microwaving time(factor B) Increases from 4minutes(-) to 6minutes(+), the bullets formed decreases from 1.9g to 0.85g.
  • When the Power setting of microwave (factor C) increases from 75%(-) to 100%(+), the bullets formed decreases from 2.15g to 1.1g
 Conclusion
  • For factor A, when the bowl diameter increases, the bullets formed decreases but it is not as significant as compared to the others factors. Hence, it is represented in the graph with the least steep gradient.
  • For factor B, when microwaving time increases, it increases the tendency of the corn being pop which reduced the amount of bullets formed. This factor is more significant than Factor A hence it is represented by a line steeper than Factor A.
  • For Factor C, When the power of the microwave increases this allows more heat to be gained and hence increases the number of corn being popped which reduces the mass of bullets formed. Being the most significant factor, the line that represent Factor C is the steepest line 
Link to Fractional Factorial excel graph (download to view the graph)


























 

Comments

Post a Comment